Binary is one of those fundamental computer science topics that looks scarier than it actually is. While we won’t be writing binary code by hand anytime soon, understanding how binary (and bytes) work is still an important skill for any programmer, especially game developers1.
What is Binary?
Binary is simply a number system that uses only two digits: 0 and 1. While we typically use the decimal system (base-10) with digits from 0-9, computers work with binary (base-2) because it maps perfectly to the on/off states of electronic circuits.
Think of it as a sequence of light switches with 0 representing “off” and 1 representing “on”2. Similar to an actual light switch, a value of 1 represents electricity flowing, while 0 represents no electricity.
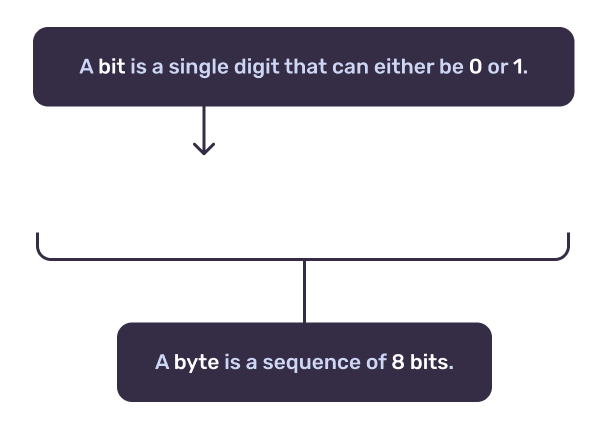
Each 0 or 1 in a binary number is called a “bit” (short for “binary digit”), and we group bits into larger units called “bytes”. For modern systems, a byte consists of 8 bits and this is the smallest unit we can address in most programming languages.
How bytes are further grouped
If you’re here, you’re probably familiar with the concept of bytes and their larger groupings like kilobytes (KB), megabytes (MB), and gigabytes (GB). But if you’re not, here’s a quick refresher.
As computers evolved, we needed ways to represent larger amounts of data. This led to the creation of larger units of measurement, which are based on powers of 2 (we’ll get to why in a moment). Here’s a quick reference for the most common units:
Unit Size Approximate Value Byte (B) 8 bits 256 values Kilobyte (KB) 1,024 bytes 1 thousand bytes Megabyte (MB) 1,024 KB 1 million bytes Gigabyte (GB) 1,024 MB 1 billion bytes Terabyte (TB) 1,024 GB 1 trillion bytes You might be wondering why we use 1,024 instead of 1,000 for these units. It’s because 1,024 is 2 to the power of 10 (2¹⁰), which is a nice round number in binary. This is why we often see the term “kibibyte” (KiB) used to refer to 1,024 bytes, as it explicitly indicates the binary definition3.
Counting in Binary
With a basic explanation of binary out of the way, let’s look at how we count using the “base-2” binary system. We start at the far right side of a byte and move left. Aside from the first (rightmost) bit, each position represents a power of 24.
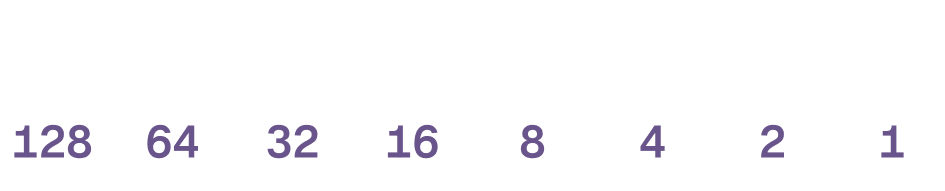
This image demonstrates the value represented by each bit in a byte.
So with all values set to 0, if the rightmost bit is also 0 then the total value represented by our byte is… 0. Easy enough. If that same bit is set to 1, then the value represented by our byte is 1. Still easy.
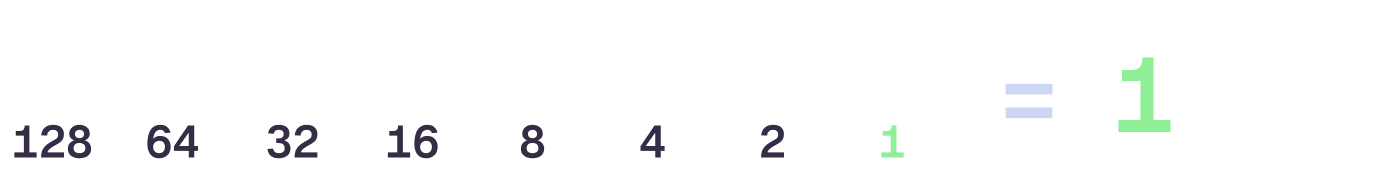
As we move left, the next bit represents either 0 or 2. With all bits set to 0 again, the value of our byte is still 0. If we set the second bit to 1, then the value represented by our byte is now 2.
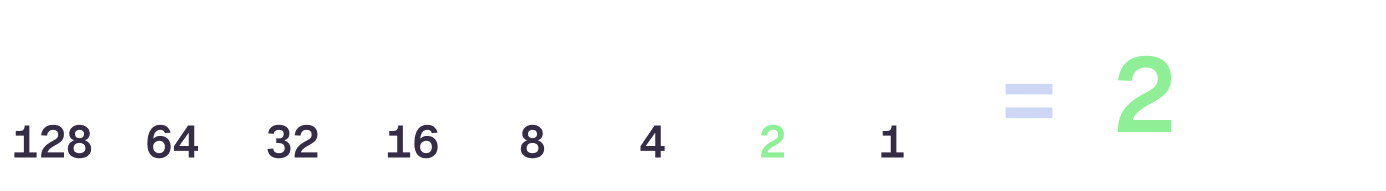
Now… if we set both the first and second bits to 1, we add them together, effectively giving us 1 + 2 — meaning the value of our byte is now 3. This pattern continues as we move left, with each bit representing a different power of 2, so the third bit represents 4, the fourth bit represents 8, and so on.
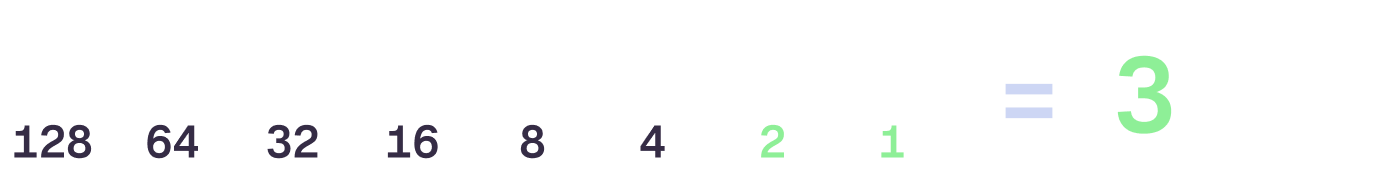
Let’s look at one more example. Let’s set all the bits to 1, meaning every bit is “on” and contributes to the total value. This means we have 1 + 2 + 4 + 8 + 16 + 32 + 64 + 128, which gives us a total of 255.
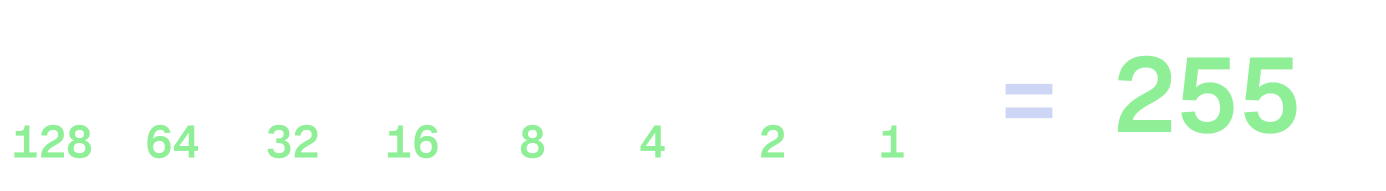
This is the maximum value we can represent with a single byte, as the next bit would represent 256, which would require a second byte. This leads us to the next topic of how bytes can be used together to represent larger values.
It’s all about the context
We can group multiple bytes together to represent larger numbers or entirely different types of data all together. How bytes are interpreted depends on the context in which they’re used. For example, a byte can represent a single character in ASCII encoding or part of a larger piece of data, like a multi-byte integer.
In many programming languages, when you see int, what you’re actually seeing is a 32-bit, or 4-byte, integer. This means we tack on bytes to our byte to represent larger values. There are other common types of integers that you might see in programming languages, like short (2 bytes) and long (8 bytes)5. The important thing to remember is that the more bytes we use, the larger the number we can represent.
| Common Name | Size (bits) | Max Value |
|---|---|---|
byte | 8 | 255 |
short | 16 | 65,535 |
int | 32 | 4,294,967,295 |
long | 64 | 18,446,744,073,709,551,615 |
For the sake of simplicity, let’s use short throughout the rest of our explanations, since it only adds a second byte for us to work with. If we set the first bit of our second byte to 1, we can represent a value of 256.
Endianess: The order of bytes
There’s just one little snag to this whole thing. When more bytes are involved, what’s the order in which we read them? This is called “endianness” and there are two options for how to do this: “big-endian” and “little-endian”.
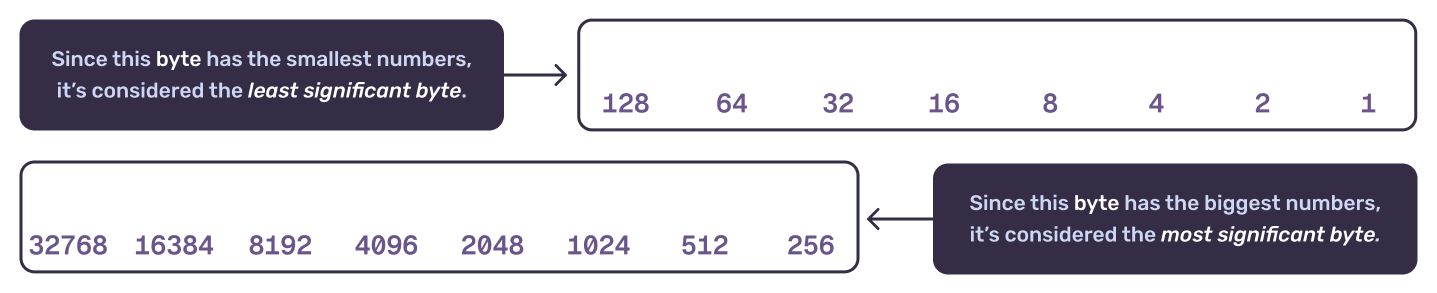
Whatever byte is biggest is the “most significant byte” and whatever byte is smallest is the “least significant byte”.
In big-endian, the most significant byte (the one that represents the largest value) is stored first. This is like reading a book from the first page to the last. Given that we read bits from right to left already, this is pretty straight forward. Let’s use the example of 259 to illustrate this.
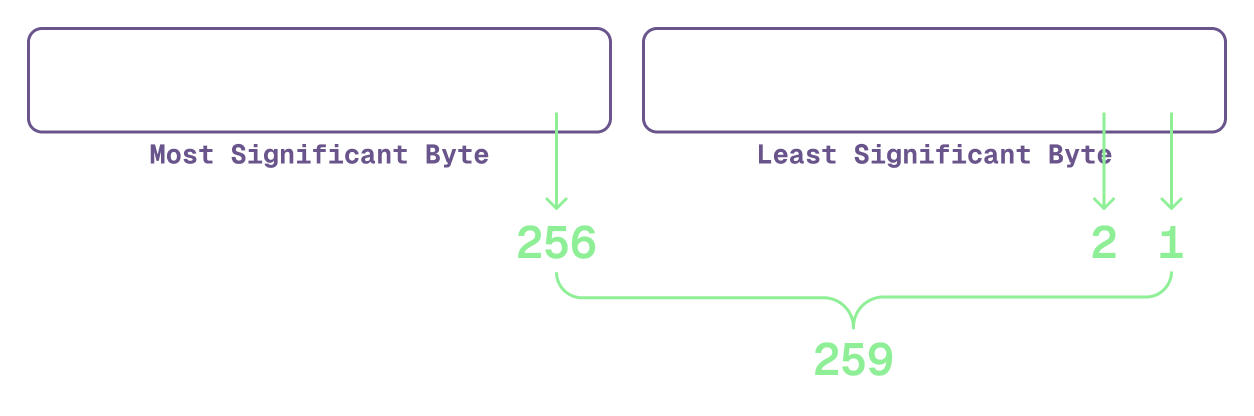
In little-endian, the least significant byte (the one that represents the smallest value) is stored first. This is like reading a book from the last page to the first. You still read the bits of each byte from right to left, but the bytes themselves are stored in reverse order.
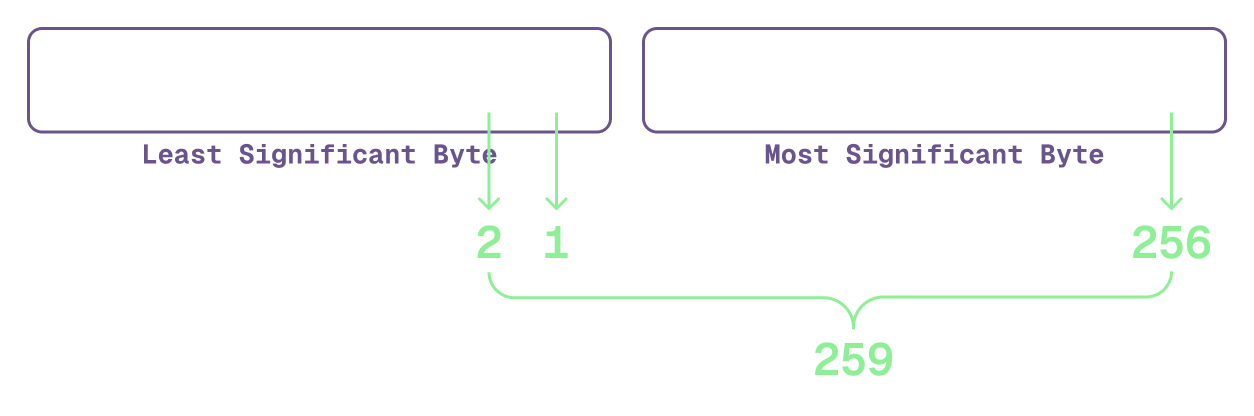
There’s a few reasons why you might want to use one over another. If you’re creating a file format, you might want to use big-endian so that it’s easier for humans to read. If you’re working with a network protocol, you might want to use little-endian so that the data is more compact.
Signed vs Unsigned Integers
Okay, we know how to count in binary and we know how to group bytes together. Great. But what if we want to represent a negative number? This is where “signed” integers come in. In our examples so far we’ve only used “unsigned” integers, which can only represent positive numbers.
A signed integer uses the first bit of the most significant byte to represent the sign of the number6. If that bit is 0, the number is positive. If that bit is 1, the number is negative.
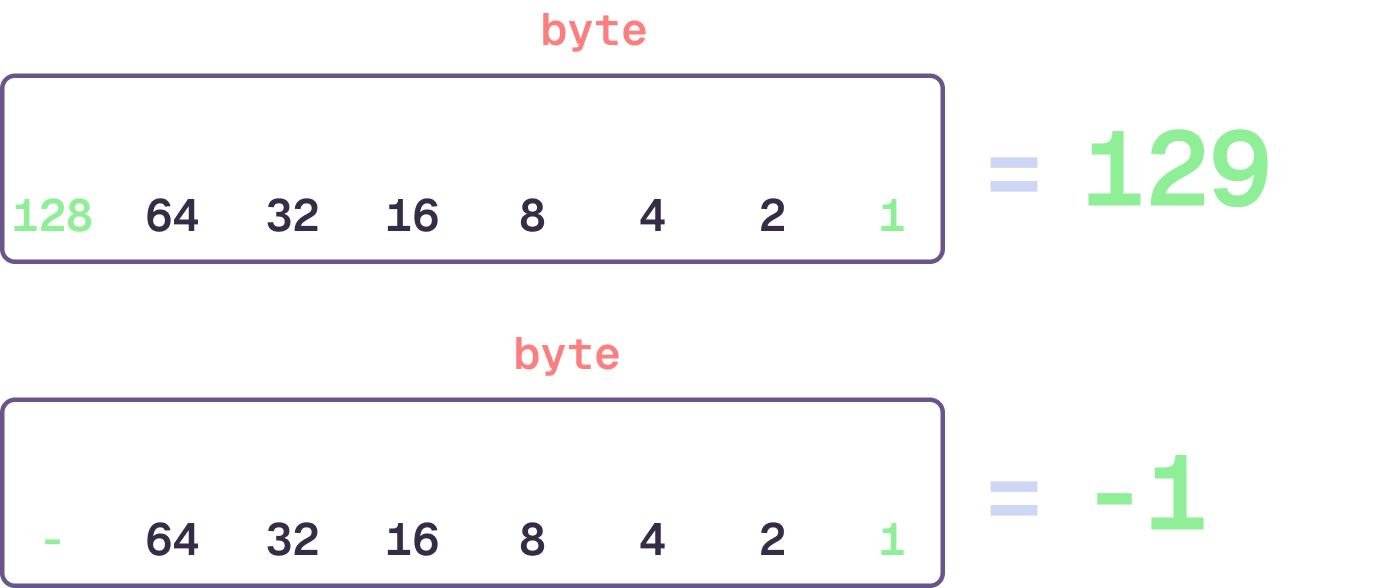
When the largest bit in a “signed” integer type is set to 1, the number is negative.
There’s a catch, though. Since we use our largest bit to tell us if the number is negative or not, we can only represent half of the total value. So for a single byte, instead of being able to represent 0 to 255, we represent -128 to 127.
| Type | Min Value | Max Value |
|---|---|---|
byte | -128 | 127 |
short | -32,768 | 32,767 |
int | -2,147,483,648 | 2,147,483,647 |
long | -9,223,372,036,854,775,808 | 9,223,372,036,854,775,807 |
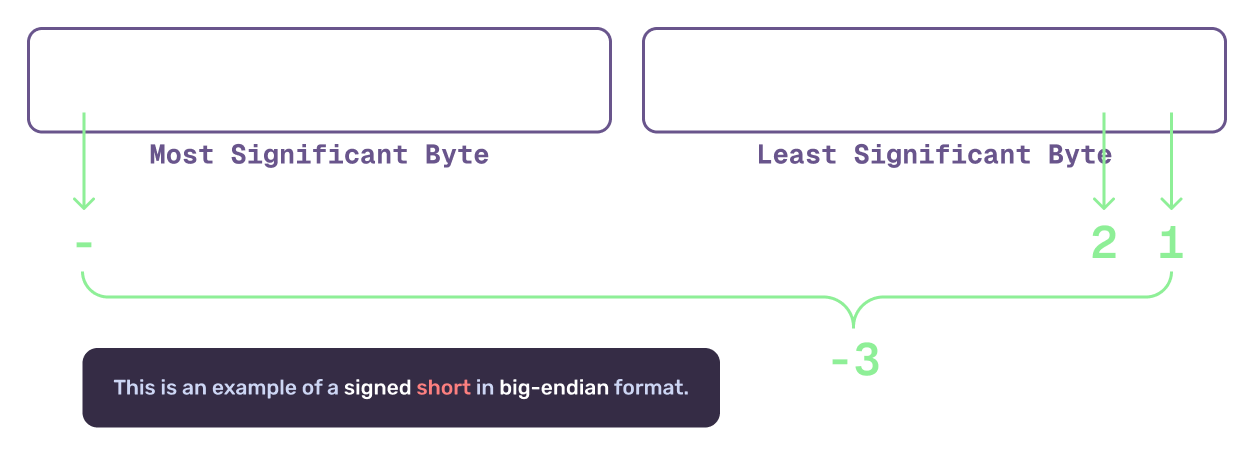
Once again, it’s important to note that the “sign bit” is the largest bit in the most significant byte. So if you’re using a short in big-endian, the sign bit is the first bit on the left byte. If you’re using a short in little-endian, the sign bit is the first bit on the right byte.
”I know kung-fu”
And that’s it! While there’s absolutely a lot more we can do with binary, these are the critical concepts that will help you understand the 1s and 0s that we associate with computers. Understanding this will allow us to explore more advanced topics related to binary and bytes in future articles.